-
Best Australian Pokies Best Payout
Play Free 777 Pokies Online
What Are the Best Australian Pokies to Win Big On
What Are the Best Online Pokies with Low Minimum Deposits for Real Money in Australia
New Australian Pokies Accepting PayID
What Are the Best Strategies to Win in Online Pokies with Bonus Rounds in Australia
Tips for Winning Top Australian Pokies
What Online Casinos Offer Free Play Pokies with Welcome Bonuses in Australia
Australian Slot Games
Payout Ratio Pokies with Welcome Bonus
a. What does the p-value mean, and how would the reader interpret this value in relation to the conclusions of the study?
b. What does the t -value measure?
What does the p-value mean
Part 1
1. You are reading a study comparing the income of first-year nursing students versus first-year respiratory students. The results section states, “the p-value is .04; the t value is 2.14.”
a. What does the p-value mean, and how would the reader interpret this value in relation to the conclusions of the study?
b. What does the t -value measure?
2. Write a brief paragraph comparing and contrasting the p-value and confidence interval involved in inferential statistics.
3. using the article from Chapter 3 (Appendix A-3), write a paragraph explaining why no significance was found between leg length discrepancy and type of hip arthroplasty. Article—Leg Length Discrepancy in Cementless Total Hip Arthroplasty (Christopher N.Peck, Karan Malhotra, Winston Y. Kim)
Part 2
Develop a table analyzing the connections between the results and conclusions from the fictional study article in Appendix B (Demographic Characteristics as Predictors of Nursing Students’ Choice of Type of Clinical Practice) The table should have a column for short statements or quotes for each discrete result and a second matching column for each discrete conclusion.
Please use the template attached below for part 1 and turn an addition Word or Excel and for part 2
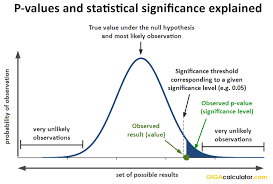
P values determine whether your hypothesis test results are statistically significant. Statistics use them all over the place. You’ll find P values in t-tests, distribution tests, ANOVA, and regression analysis. P values have become so important that they’ve taken on a life of their own. They can determine which studies are published, which projects receive funding, and which university faculty members become tenured!
Ironically, despite being so influential, P values are misinterpreted very frequently. What is the correct interpretation of P values? What do P values really mean? That’s the topic of this post!
P values are a slippery concept. Don’t worry. I’ll explain p-values using an intuitive, concept-based approach so you can avoid making a widespread misinterpretation that can cause serious problems.
What Is the Null Hypothesis?
P values are directly connected to the null hypothesis. So, we need to cover that first!
In all hypothesis tests, the researchers are testing an effect of some sort. The effect can be the effectiveness of a new vaccination, the durability of a new product, and so on. There is some benefit or difference that the researchers hope to identify.
 However, it’s possible that there actually is no effect or no difference between the experimental groups. In statistics, we call this lack of an effect the null hypothesis. When you assess the results of a hypothesis test, you can think of the null hypothesis as the devil’s advocate position, or the position you take for the sake of argument.
However, it’s possible that there actually is no effect or no difference between the experimental groups. In statistics, we call this lack of an effect the null hypothesis. When you assess the results of a hypothesis test, you can think of the null hypothesis as the devil’s advocate position, or the position you take for the sake of argument.
To understand this idea, imagine a hypothetical study for medication that we know is entirely useless. In other words, the null hypothesis is true. There is no difference at the population level between subjects who take the medication and subjects who don’t.
P values Are NOT an Error Rate
Unfortunately, P values are frequently misinterpreted. A common mistake is that they represent the likelihood of rejecting a null hypothesis that is actually true (Type I error). The idea that P values are the probability of making a mistake is WRONG! You can read a blog post I wrote to learn why P values are misinterpreted so frequently.
You can’t use P values to directly calculate the error rate for several reasons.
First, P value calculations assume that the null hypothesis is correct. Thus, from the P value’s point of view, the null hypothesis is 100% true. Remember, P values assume that the null is true, and sampling error caused the observed sample effect.
Second, P values tell you how consistent your sample data are with a true null hypothesis. However, when your data are very inconsistent with the null hypothesis, P values can’t determine which of the following two possibilities is more probable:
- The null hypothesis is true, but your sample is unusual due to random sampling error.
- The null hypothesis is false.
To figure out which option is right, you must apply expert knowledge of the study area and, very importantly, assess the results of similar studies.
Going back to our medication study, let’s highlight the correct and incorrect way to interpret the P value of 0.03:
- Correct: Assuming the medication has zero effect in the population, you’d obtain the sample effect, or larger, in 3% of studies because of random sample error.
- Incorrect: There’s a 3% chance of making a mistake by rejecting the null hypothesis.
Yes, I realize that the incorrect definition seems more straightforward, and that’s why it is so common. Unfortunately, using this definition gives you a false sense of security, as I’ll show you next.
Related posts: See a graphical illustration of how t-tests and the F-test in ANOVA produce P values.
Attachments
